Okay, so you’re going to have some basic knowledge of calculus for this one. I might make an explanation that’ll be accessible to everyone at some point. This is not that point.
Marden’s Theorem is my favorite mathematical theorem. It isn’t particularly useful, it isn’t particularly related to anything I’m studying. Hell, I don’t expect most actual mathematicians to know it. It’s just something I sort of stumbled upon. But it demonstrates why I think maths is beautiful.
The theorem is as follows. Consider a cubic polynomial (something of the form ax^3+bx^3+cx+d for constants a,b,c,d and a is not 0). Cubic polynomials have three roots (values of x where the polynomial becomes 0). We can plot the three roots as points on the complex plane. For any three points we can make a triangle with those three points as vertices. Inside any triangle it is a known fact that there is a unique oval inside the triangle such that the oval is tangent to the midpoint of each of the edges.
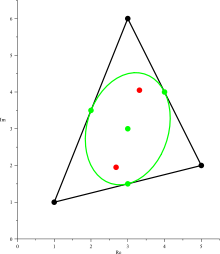
If one took the foci of the oval (the two points whose distance to points on the edge add up to the same value, no matter which edge point is picked), they are the roots for the derivative of your original cubic.
Isn’t that magical? We started with an object from calculus, applied some geometric properties of triangles and ovals, and ended with an answer to a calculus question! Math is an incredibly interconnected discipline, with one segment of each field affecting wildly separate fields. Facts about one discipline can open new doors in other seemingly unrelated things. Geometry and Calculus are different fields, but in Marden’s Theorem they are joined in this simple, completely unintuitive way and I think that’s beautiful.