So for those of you who don’t know, there is a mathematical function known as a Factorial. It’s denoted by “!”. So I could write that 3!=6. And what a factorial does to a number “n” is that it multiplies all positive whole numbers less than or equal to “n.” So 3!=3 x 2 x 1=6. Factorials are fun because they grow so damn fast. 10!=3,628,800. 61! is a number bigger than the number of atoms in the entire universe. Just 61 factorial!!!
A lot of this you might have learned in high school. They’re a fun function, used in a lot of things, but I’m going to answer the following question. What is 1.5! ? It seems like a daft question. It’s the product all positive whole numbers less than or equal to 1.5, so by that definition shouldn’t it be 1? Since the only One could certainly “extend” the factorials in such a way. In doing so you’d get a function that looks like this.
(I’ll make a picture eventually, for now imagine a graph that looks like a staircase, complete with a lot of breaks in the graph)
But such an extension isn’t particularly interesting nor particularly useful. It doesn’t maintain a lot of the “nice” properties of a factorial. Notably, we would like our function to behave “nicely” under most operations. (We want it to be analytic and log convex for those of you who know what those words mean) and we want (x)(n\x-1)!=n! for all values of x. But if the answer to 1.5! isn’t one what is it then?
The answer is that 1.5! is the square root of pi.
Yup. This nice, seemingly normal factorial has a value simultaneously so messy (the square root of pi?? What even is that??) and so clean. The function that extends the factorials nicely is called the Gamma function. I’m not going to tell you what it is, though if you understand indefinite integrals you should be able to understand most of it. But here’s a graph of what it looks like.
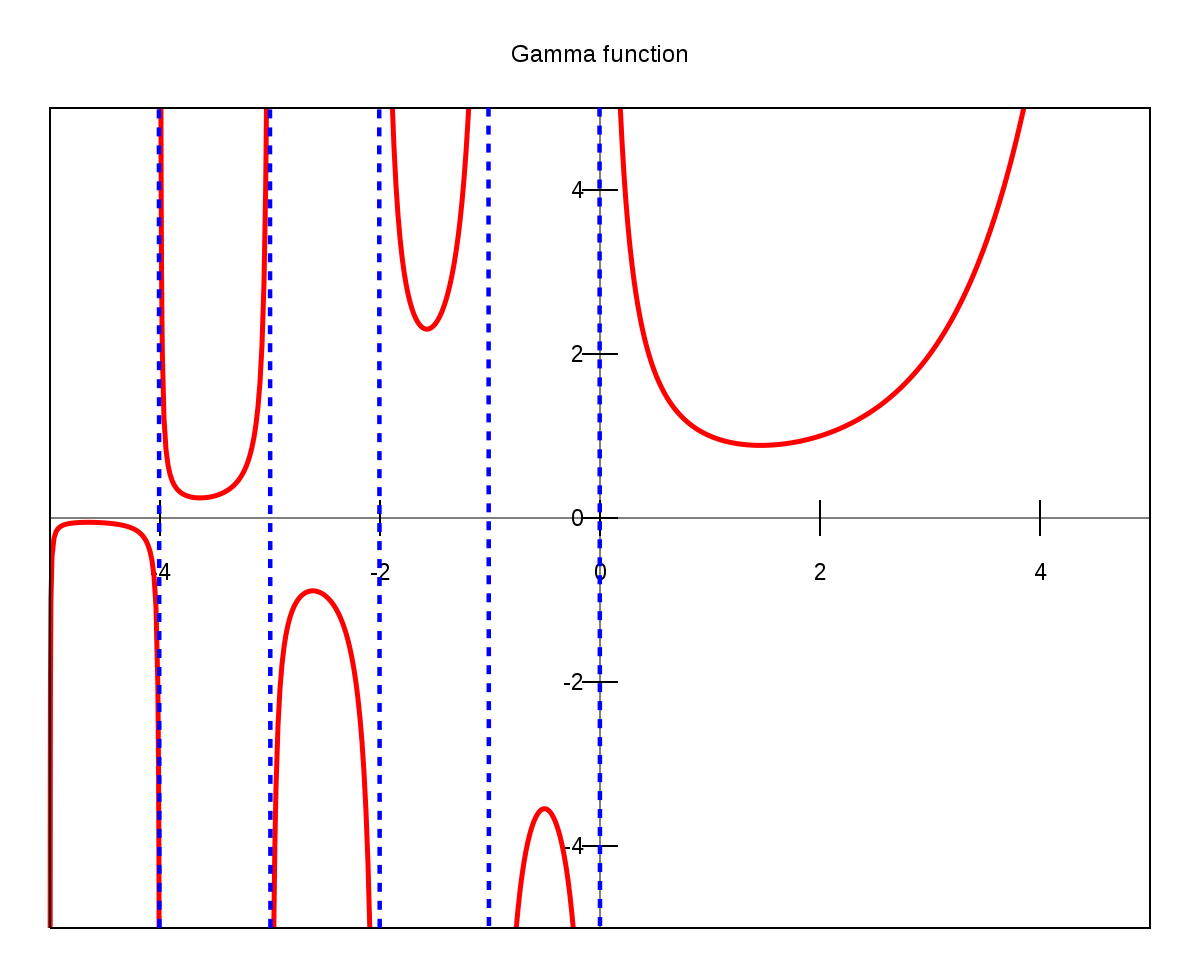
(Note, that technically Gamma(x)=x+1!, so to get the factorials you have to shift everything left by one.)